Bayes’ Rule
In the previous section, we studied conditional probability \[P(B|A) = \displaystyle\frac{P(A \text{ and } B)}{P(A)}\] and we talked about how the inverse probabilities \(P(A|B)\) and \(P(B|A)\) are almost never equal. In this section, we discuss how to properly think and calculate that inverse probability.
Another look at conditional probability is \[P(A \text{ and } B) = P(B|A) \cdot P(A)\] This is read as “The probability of the intersection \(A\) and \(B\) is the probability of event \(B\) conditioned on event \(A\).”
Moreover, if we consider how if event \(B\) is dependent on event \(A\), then sometimes \(B\) happens when \(A\) happens and sometimes when \(A\) does not occur. More succinctly, the total probability of event \(B\) is \[P(B) = P(B|A) \cdot P(A) + P(B|A^{c}) \cdot P(A^{c})\]
Staring with the conditional probability formula \[P(B|A) = \displaystyle\frac{P(A \text{ and } B)}{P(A)}\] Bayes’ Rule combines the ideas of conditioned probability and total probability as \[P(A|B) = \displaystyle\frac{P(A \text{ and } B)}{P(B)} = \displaystyle\frac{P(B|A) \cdot P(A)}{P(B|A) \cdot P(A) + P(B|A^{c}) \cdot P(A^{c})}\]
A Deep Dive
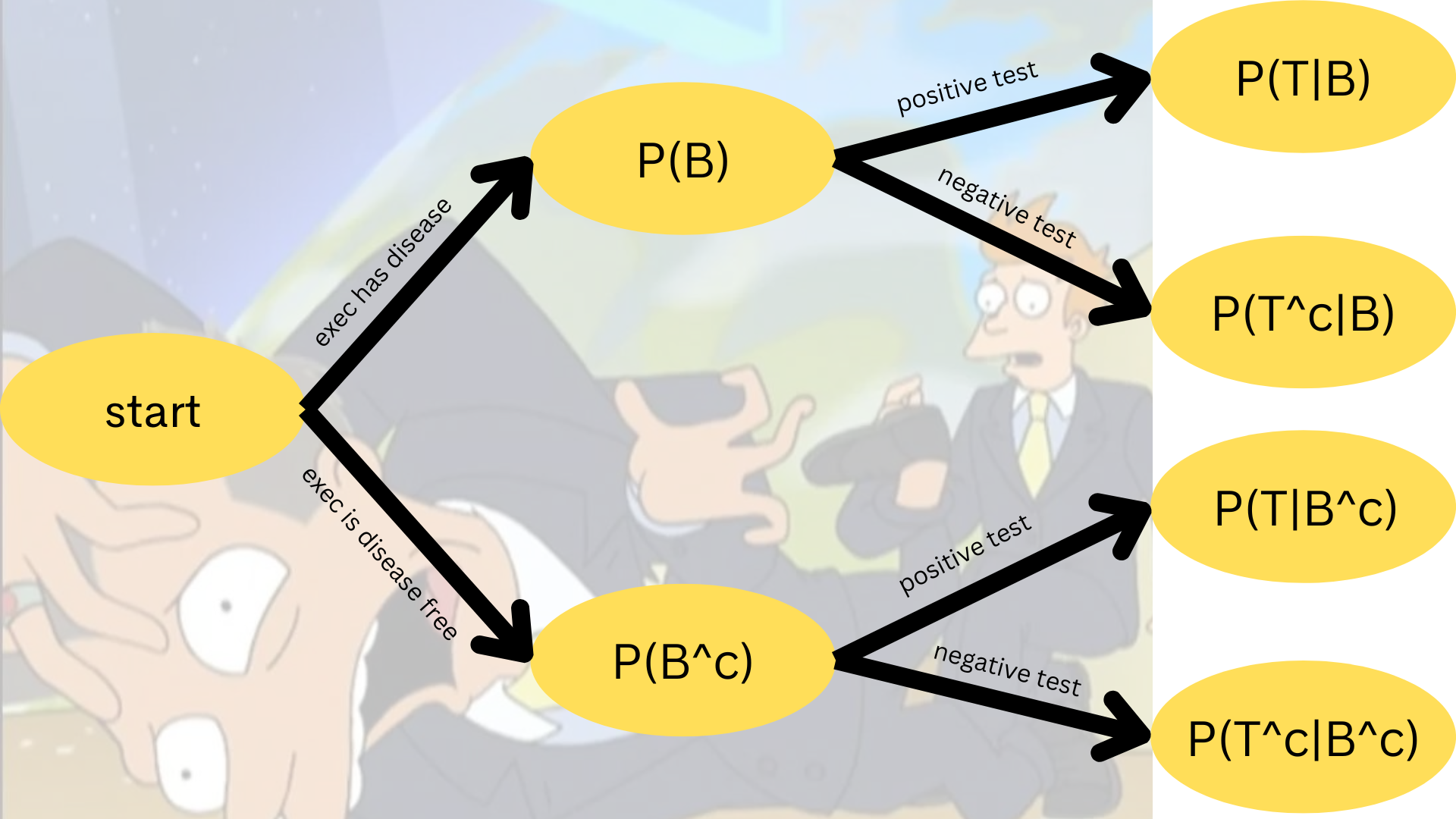
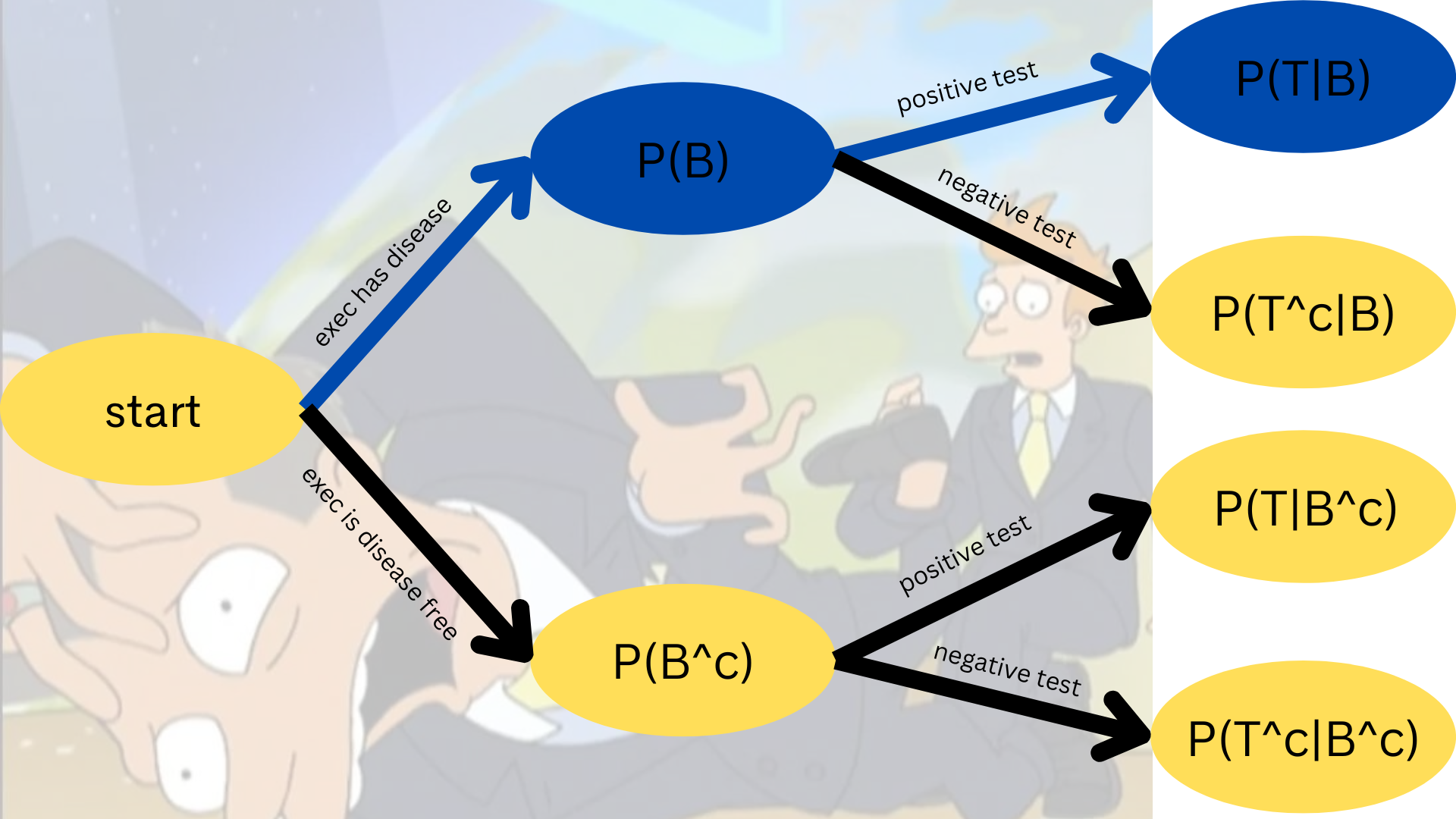
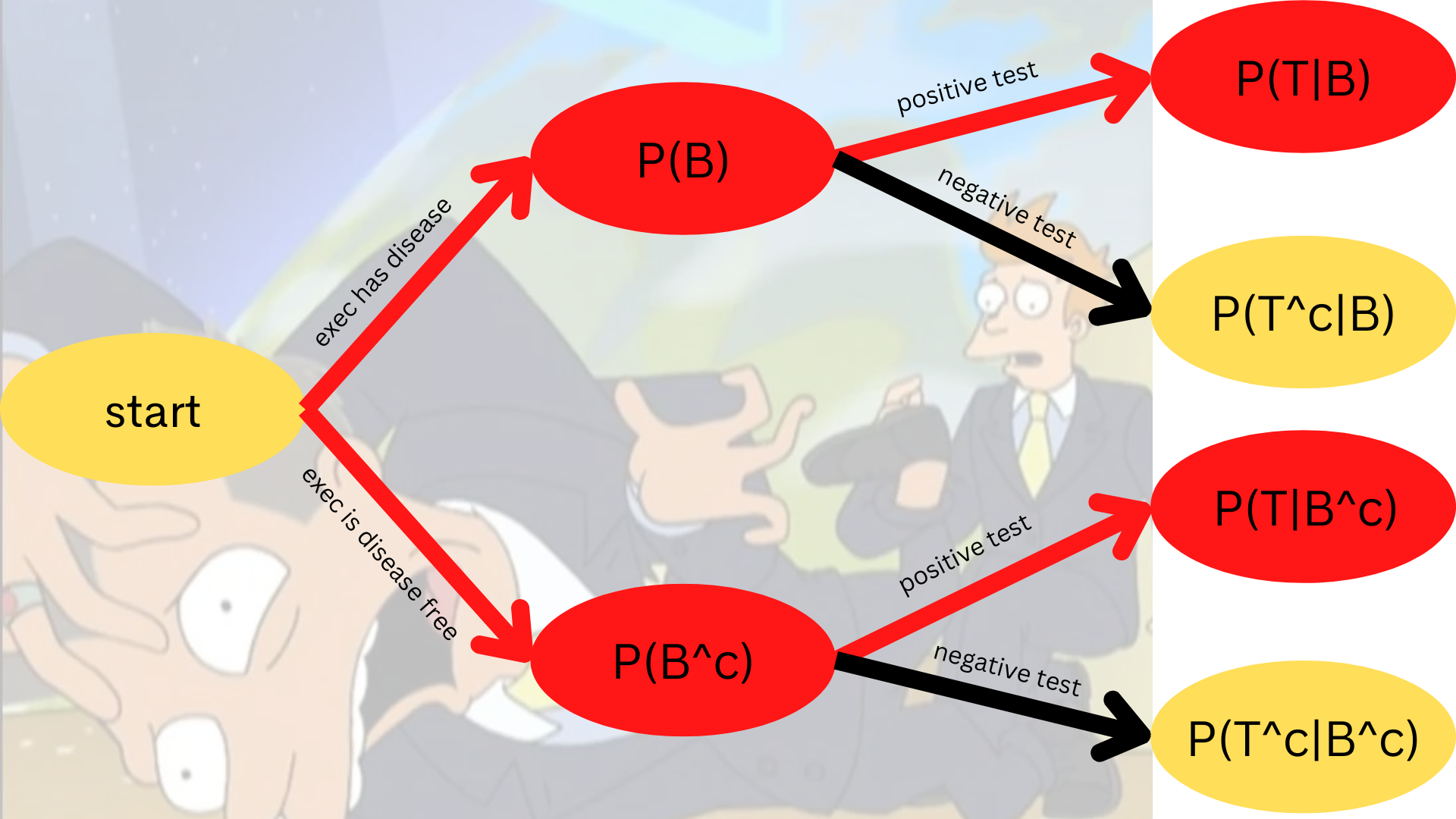
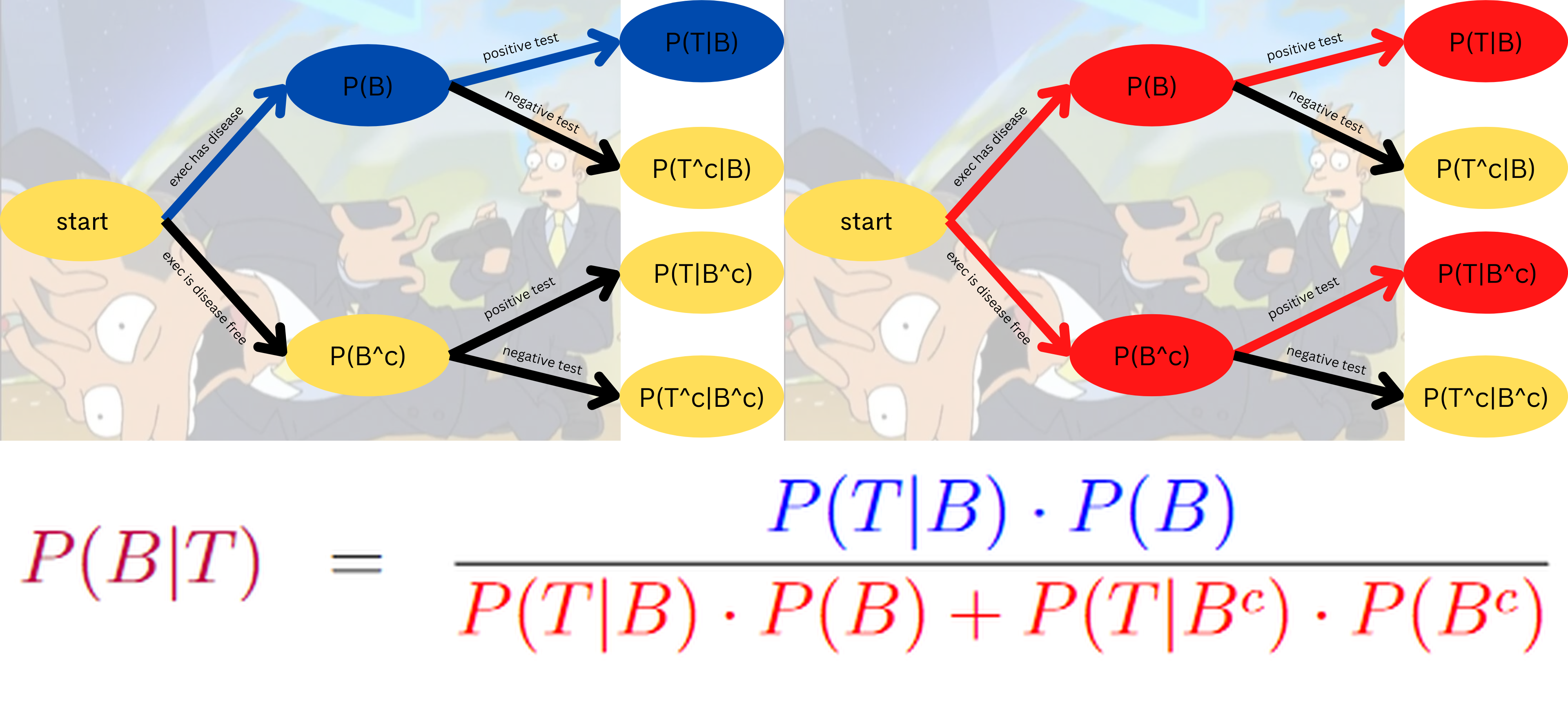
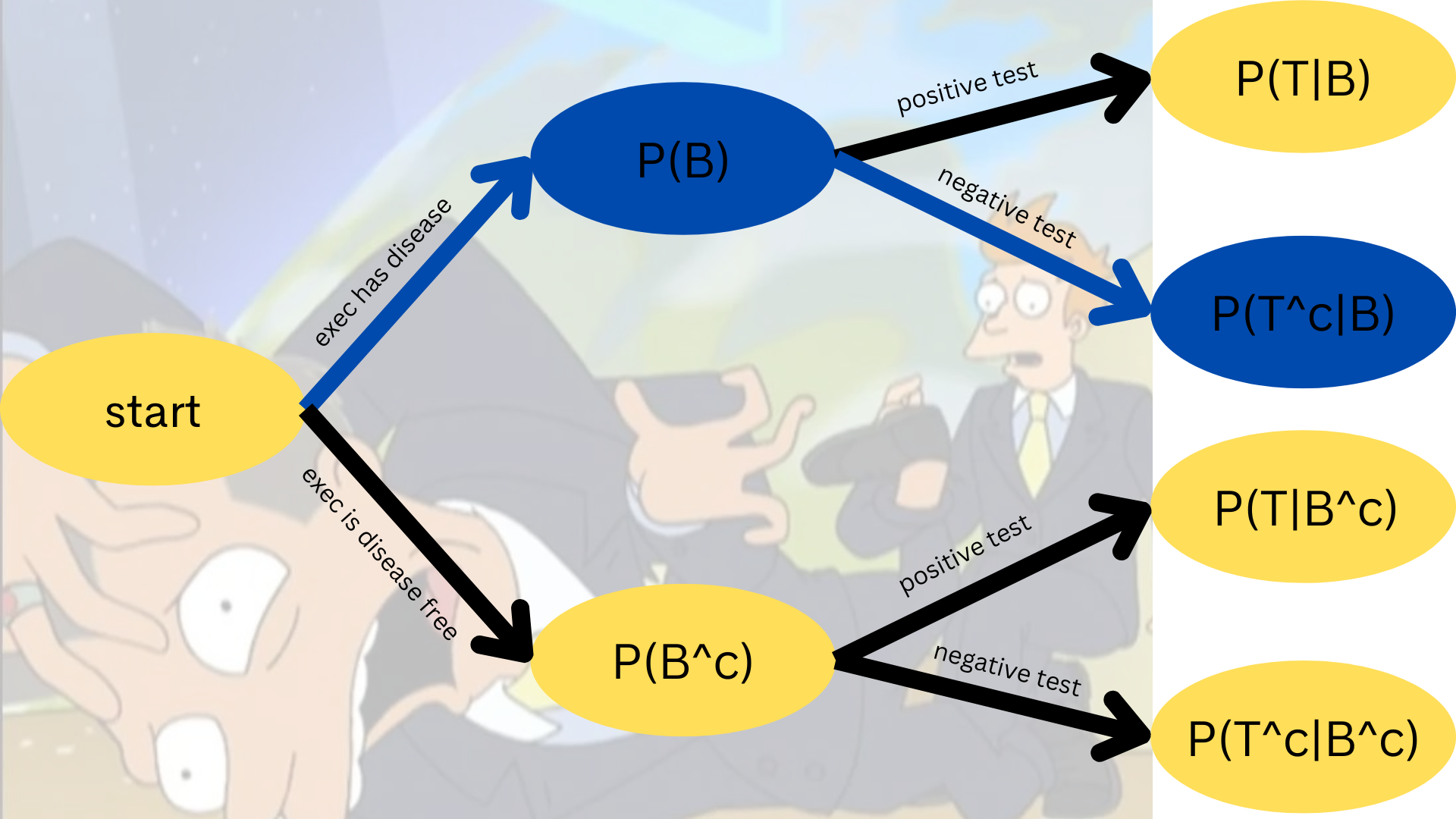
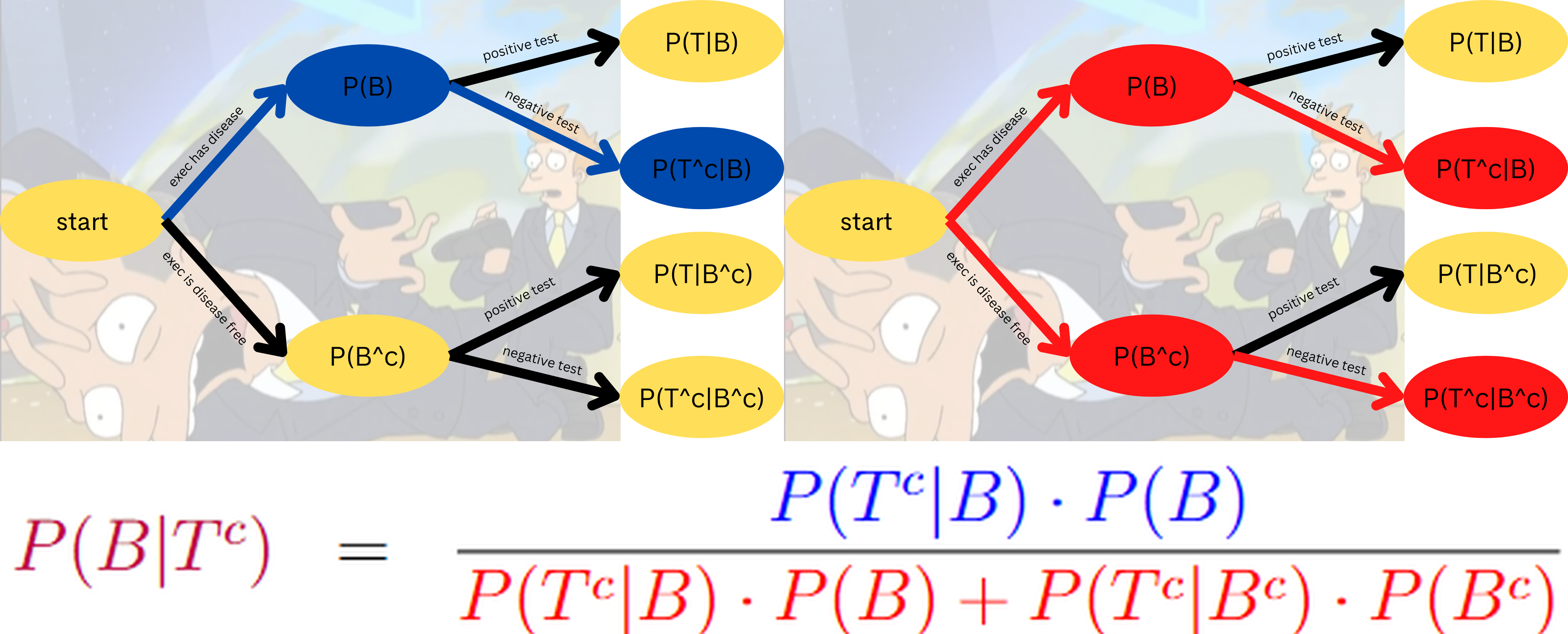
An executive has their blood tested for boneitis. Let \(B\) be the event that an executive has the disease, and let \(T\) be the event that the test returns positive. Laboratory trials yielded the following information:
\[P(T|B) = 0.70 \quad\text{and}\quad P(T|B^{c}) = 0.10\]
Assume a prior probability of \(P(B) = 0.0032\). Compute \(P(B|T)\)
More Practice
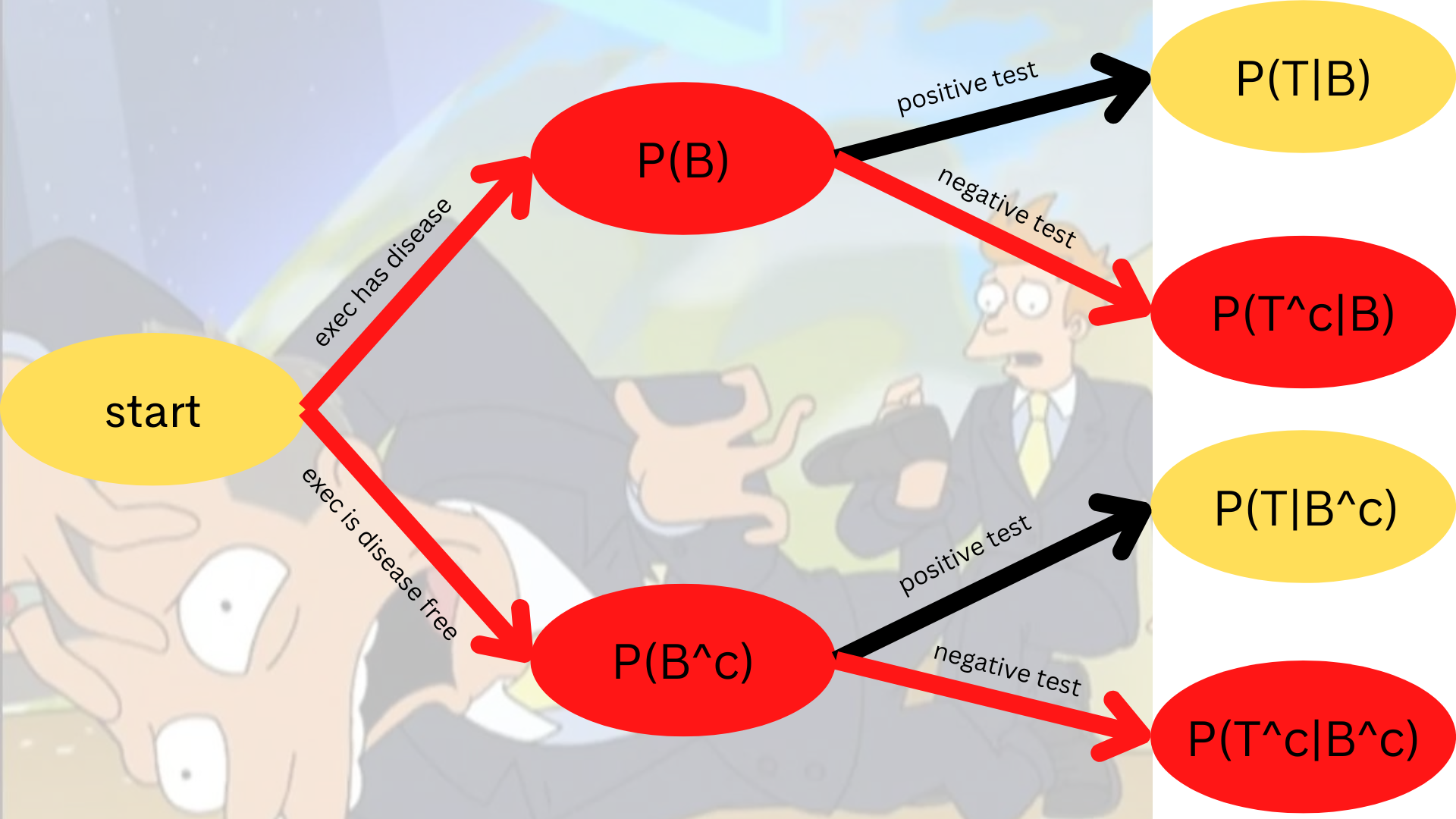
An executive has their blood tested for boneitis. Let \(B\) be the event that an executive has the disease, and let \(T\) be the event that the test returns positive. Laboratory trials yielded the following information:
\[P(T|B) = 0.70 \quad\text{and}\quad P(T|B^{c}) = 0.10\]
Assume a prior probability of \(P(B) = 0.0032\). Compute \(P(B|T^{c})\)
Example: Monty Hall Problem
Monty Hall asks you to choose one of three doors. One of the doors hides a prize and the other two doors have no prize. You state out loud which door you pick, but you don’t open it right away.
“Monty opens one of the other two doors, and there is no prize behind it.“At this moment, there are two closed doors, one of which you picked. The prize is behind one of the closed doors, but you don’t know which one. Monty asks you, ‘Do you want to switch doors?’”
- switch doors
- do not switch doors
Looking Ahead
- due Fri., Jan. 27:
- WHW2
- JHW0
- CLO (survey)
- and the before-lecture quizzes
Exam 1 will be on Wed., Mar. 1
