19: Covariance

Setting

We will once again visualize the act of ordering food at In-n-Out.

• $X$: number of fries orders
• $Y$: number of beef patties ordered

joint PMF

In-n-Out

Independence

Are $X$ and $Y$ independent?

Covariance

True or False? $\text{Var}(X+Y)=\text{Var}(X)+\text{Var}(Y)$

False. In general,

$$\text{Var}(X+Y)=\text{Var}(X)+\text{Var}(Y)+2(\text{E}[XY]-\text{E}[X]\text{E}[Y])$$

Motivation for Independence

As you probably suspected, $\text{Var}(X+Y)$ does equal $\text{Var}(X)+\text{Var}(Y)$ if $X$ and $Y$ are independent (exercise left to reader).

Covariance

We define the covariance of random variables as

$$\text{Cov}(X,Y)=\text{E}[XY]-\text{E}[X]\text{E}[Y]$$

Derek’s Intuition

As an analogy, the random variables somewhat act like waves in that they can work together and grow or somewhat cancel each other out.

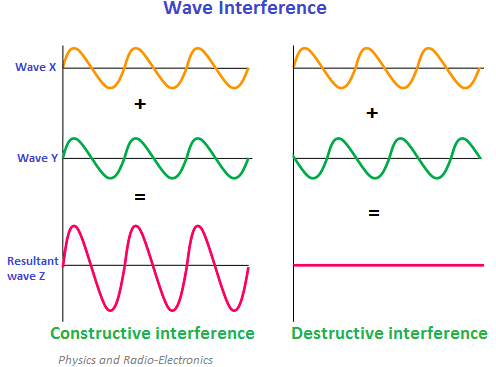
• Image source: https://www.physics-and-radio-electronics.com/physics/waveinterference.html

The Pythagorean Theorem of Statistics

• Image credit: Bioinformatics professor Dr. David Ardell

Covariance

• Compute the covariance in the In-n-Out setting

Continuous Joint Probability Distribution Functions

We will once again visualize the act of ordering food at In-n-Out.

• $X$: number of fries orders
• $Y$: number of beef patties ordered

with joint PDF

$$f(x,y)=\frac{1}{30}(x+y)e^{-x}{e}^{-y/5}$$

• Are $X$ and $Y$ independent?

• Compute the covariance in the In-n-Out setting

In-n-Out

Looking Ahead

• due Fri., Mar. 10:

  • WHW7
  • LHW6
  • Internet Connection (survey)

• Exam 2 will be on Mon., Apr. 10

• no lecture on Mar. 10, Mar. 24

tweet source