Linear Conversion
Let
We know that the conversion formula is
Range Rule of Thumb
Recall
- About 67 percent of data falls within one standard deviation of the mean
- About 95 percent of data falls within two standard deviations of the mean
We had computed
Build range-rule-of-thumb intervals for the Merced high temperatures in Fahrenheit and in Celsius.
Distributions
Determine the distribution and density functions for
Change of Coordinates
Let
where
If
Nonlinear Transformations
Let
Compare
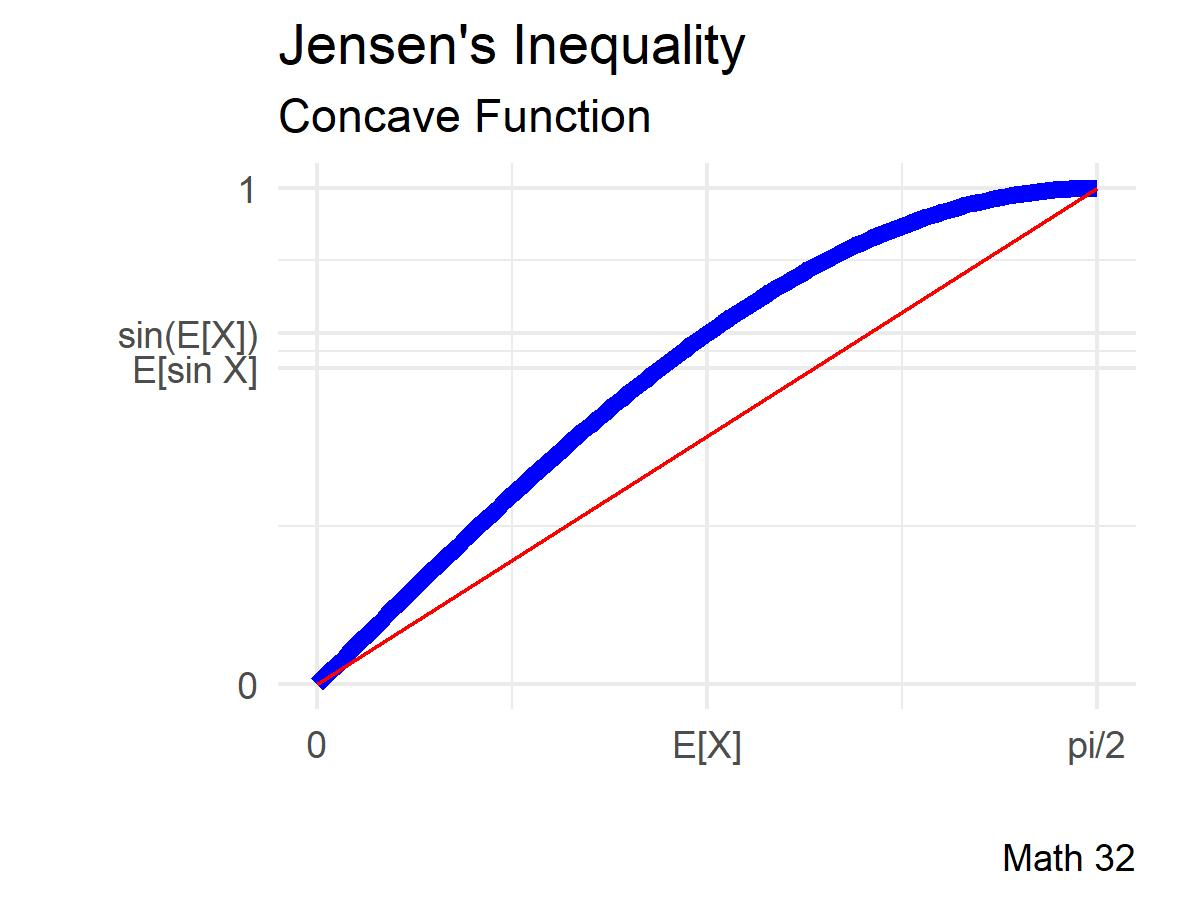
Suppose that a disease outbreak can be modeled where
Compare
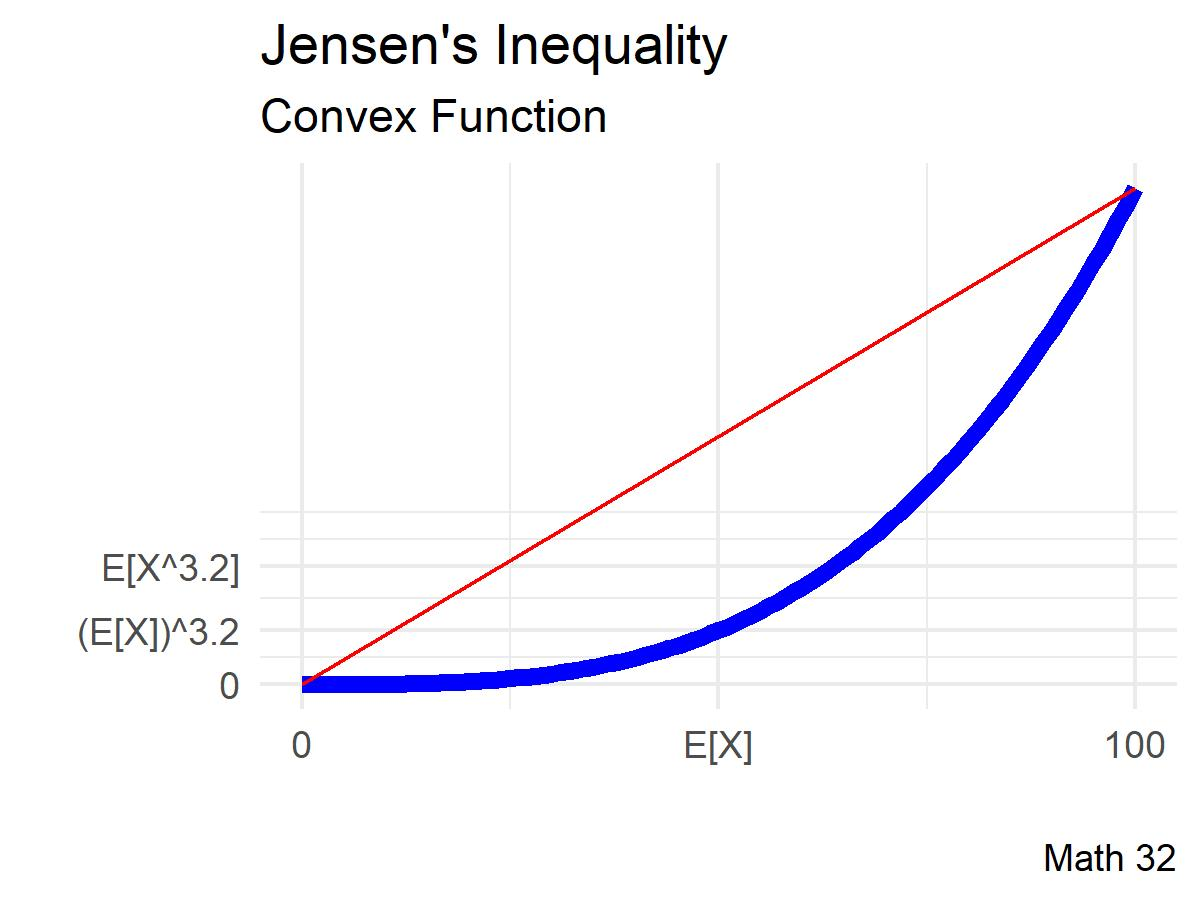
The previous two examples were demonstrations of , which states that
- If
where the equal signs are not included when the function
Looking Ahead
due Fri., Mar. 17:
- WHW8
- LHW7
no lecture on Mar. 24, Apr. 3
Exam 2 will be on Mon., Apr. 10
Misc
