library("tidyverse")── Attaching packages ─────────────────────────────────────── tidyverse 1.3.2 ──
✔ ggplot2 3.4.0 ✔ purrr 1.0.1
✔ tibble 3.1.8 ✔ dplyr 1.0.10
✔ tidyr 1.2.1 ✔ stringr 1.5.0
✔ readr 2.1.3 ✔ forcats 0.5.1
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()In order to introduce probability concepts, you will notice that many sections of this book start out by talking about simple situations such as flipping a coin or rolling a die (or rolling a pair of dice). This is to ease the reader into more complicated examples.
A possibility space is a set of all of the possible outcomes.
Consider rolling one six-sided die. For each of the following events, list their possible ways, and then find their probabilities:
At first, we consider simply adding up the probabilities to compute the probability of the union of the probabilities:
\[P(A \cup B) = P(A) + P(B) = ?\] ## Inconsistent?
So far,
\[P(A \cup B) = P(A) + P(B) = 100\%\] What went wrong? (Discuss with a neighbor)
The union of sets A and B is the set of all elements that appear either in set A OR set B \[A \cup B = \{x : x \in A \text{ OR } x \in B\}\]
The intersection of sets A and B is the set of all elements that appear both in set A AND set B \[A \cap B = \{x : x \in A \text{ AND } x \in B\}\]
We observe that there was an overlap in the calculation. Since some elements were counted twice, we can compensate by subtracting one copy of that overlap. This notion is called the Inclusion-Exclusion Principle
To compute the probability of a set union, we need to consider the overlapping portions. For two sets A and B, the probability of observing the union is \[P(A \cup B) = {\color{red}P(A)} + {\color{blue}P(B)} - {\color{purple}P(A \cap B)}\]
Consider rolling two six-sided dice. Find the probability that their total is 8 or the second die shows a number greater or equal to 5.
In the previous example, we assumed a notion of sampling with replacement. That is, when rolling dice, we know that a number can be repeated. In other situations were observations cannot repeat, we are sampling without replacement.
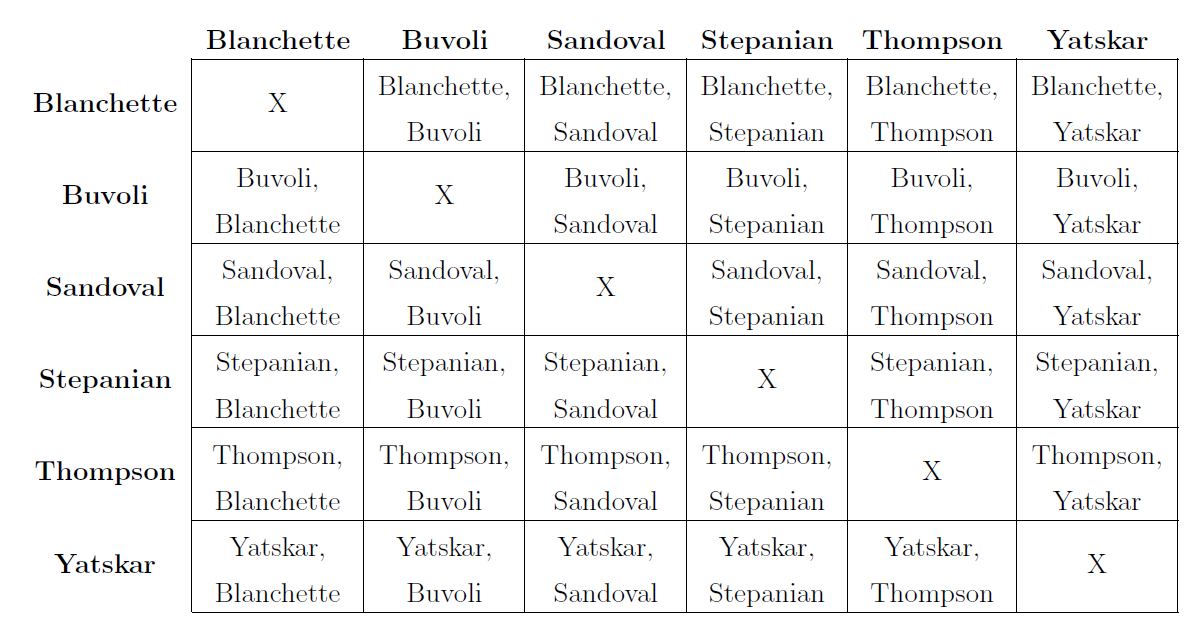
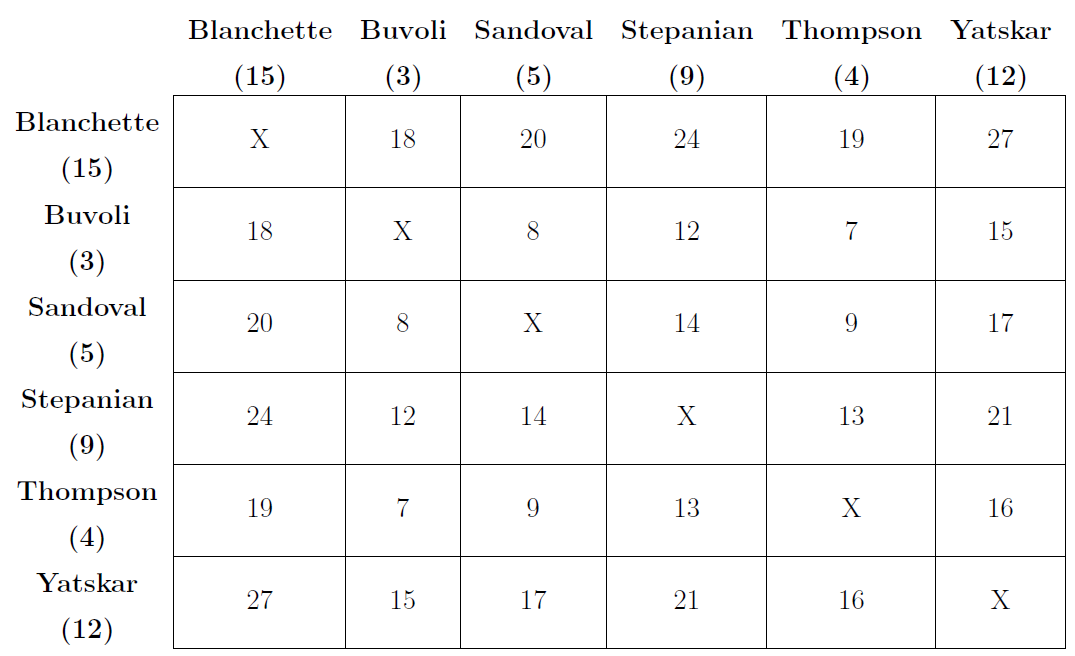
Consider a subset of the UC Merced Applied Math department with 6 faculty members—Blanchette, Buvoli, Sandoval, Stepanian, Thompson, Yatskar—must select two of its members to serve on a personnel review committee. Because the work will be time-consuming, no one is anxious to serve, so it is decided that the representatives will be selected by putting 6 slips of paper in a box, mixing them, and selecting two without replacement.
Exam 1 will be on Wed., Mar. 1
