08: Variance

Overview

\[s^{2} = \displaystyle\frac{1}{n-1}\displaystyle\sum_{i = 1}^{n} (x_{i} - \bar{x})^{2}\]

Today’s main questions are “What is variance and what is a standard deviation?” We will go through

• the formulas and calculations
• demostrations
• applications (word problems)

Notation

We tend to study a relatively small sample to understand the behavior of a much larger population.

Example: Nathan’s Hot Dog Eating Contest

Each year on July 4, the Nathan’s Hot Dog Eating Contest takes place on Coney Island in New York. The rule is simple: eat as many hot dogs (and buns) as you can in 10 minutes. The past 5 winning amounts were: 63, 70, 72, 74, 71. Compute the variance.

\[s^{2} = \displaystyle\frac{1}{n-1}\displaystyle\sum_{i = 1}^{n} (x_{i} - \bar{x})^{2}\]

Units?

square hot dogs?

Demostrations

Setup

For each of the following sets

• \(A = \{1, 2, 3, 4, 5, 6, 7\}\)
• \(B = \{3, 4, 5, 6, 7, 8, 9\}\)
• \(C = \{-3, -2, -1, 0, 1, 2, 3\}\)
• \(D = \{-9, -6, -3, 0, 3, 6, 9\}\)

we will compute the sample mean, sample median, and sample standard deviation.

R

A <- seq(1, 7, 1)
B <- A + 2
C <- seq(-3, 3, 3)
D <- 3*C

A to B

mean(A)

[1] 4

mean(B)

[1] 6

median(A)

[1] 4

median(B)

[1] 6

sd(A)

[1] 2.160247

sd(B)

[1] 2.160247

C to D

mean(C)

[1] 0

mean(D)

[1] 0

median(C)

[1] 0

median(D)

[1] 0

sd(C)

[1] 3

sd(D)

[1] 9

Standardization

\[z = \displaystyle\frac{x - \mu}{\sigma}\]

To standardize data, compute a z-score by

• subtracting by the mean
• then dividing by the standard deviation

This calculation is considered to be “unitless”, and the units are usually said as “[number of] standard deviations above/below the mean”

Most data falls within two standard deviations of the mean,

\[\text{usually } z \in (-2, 2)\]

but \(z \in (-\infty, \infty)\)

Example: Dating Website Data

Scenario 1

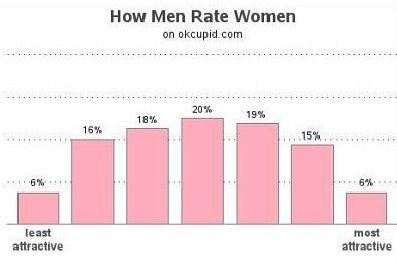
According to OkCupid data, if men rate women on a scale from 1 = “least attractive” to 7 = “most attractive”, the average score is 3.99 with a sample standard deviation of 1.6401.

• What is the \(z\)-score of a woman rated a “6”?
• What is the attractiveness score of a woman at a \(z\)-score of 1.5?

Scenario 2

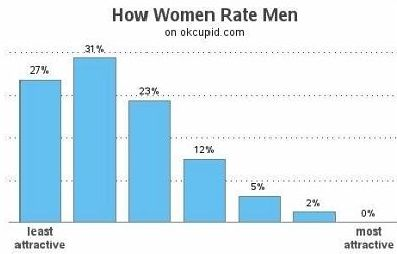
According to OkCupid data, if women rate men on a scale from 1 = “least attractive” to 7 = “most attractive”, the average score is 2.43 with a sample standard deviation of 1.2510.

• What is the \(z\)-score of a man rated a “6”?
• What is the attractiveness score of a man at a \(z\)-score of 1.5?

Looking Ahead

• due Fri., Feb. 3:
  • WHW3
  • JHW1
  • Identity Statement (short essay)
• and the before-lecture quizzes

Exam 1 will be on Wed., Mar. 1

• more information will be in the weekly announcements

source